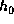Specification

In Tiger all the computations are on 64-bit words, in little-endian/2-complement representation. We use three 64-bit registers called a, b, and c as the intermediate hash values. These registers are initialized to 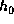which is:

      a = 0x0123456789ABCDEF
      b = 0xFEDCBA9876543210
      c = 0xF096A5B4C3B2E187

Each successive 512-bit message block is divided into eight 64-bit words x0, x1, ..., x7, and the following computation is performed to update 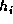to .

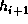This computation consists of three passes, and between each of them there is a key schedule --- an invertible transformation of the input data which prevents an attacker forcing sparse inputs in all three rounds. Finally there is a feedforward stage in which the new values of a, b, and c are combined with their initial values to give :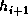

      save_abc
      pass(a,b,c,5)
      key_schedule
      pass(c,a,b,7)
      key_schedule
      pass(b,c,a,9)
      feedforward

where

1. save_abc saves the value of

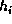
         aa = a ;
         bb = b ;
         cc = c ;
   

2. pass(a,b,c,mul) is

         round(a,b,c,x0,mul);
         round(b,c,a,x1,mul);
         round(c,a,b,x2,mul);
         round(a,b,c,x3,mul);
         round(b,c,a,x4,mul);
         round(c,a,b,x5,mul);
         round(a,b,c,x6,mul);
         round(b,c,a,x7,mul);
   

   where round(a,b,c,x,mul) is

         c ^= x ;
         a -= t1[c_0] ^ t2[c_2] ^ t3[c_4] ^ t4[c_6] ;
         b += t4[c_1] ^ t3[c_3] ^ t2[c_5] ^ t1[c_7] ;
         b *= mul;
   

   and where c_i is the ith byte of c (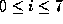). Note that we use the notation of the C programming language, where ^ denotes the XOR operator, and the notation X op= Y means X = X op Y, for any operator op. The S boxes t1 to t4 would take ten pages to publish here, so they will be published electronically along with the full source code, and made available from the authors' world wide web home pages.

3. key_schedule is

         x0 -= x7 ^ 0xA5A5A5A5A5A5A5A5; 
         x1 ^= x0; 
         x2 += x1; 
         x3 -= x2 ^ ((~x1)<<19); 
         x4 ^= x3; 
         x5 += x4; 
         x6 -= x5 ^ ((~x4)>>23); 
         x7 ^= x6; 
         x0 += x7; 
         x1 -= x0 ^ ((~x7)<<19); 
         x2 ^= x1; 
         x3 += x2; 
         x4 -= x3 ^ ((~x2)>>23); 
         x5 ^= x4; 
         x6 += x5; 
         x7 -= x6 ^ 0x0123456789ABCDEF;
   

   where << and >> are logical (rather than arithmetic) shift left and shift right operators.

4. feedforward is

         a ^= aa ;
         b -= bb ;
         c += cc ;
   

   The resultant registers a, b, c are the 192 bits of the (intermediate) hash value .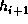

Figure 1

  
Figure 1: Outline of the compression function of Tiger

describes the compression function. In this figure the black area denotes the affected registers, where the slanted lines point to the affecting bytes in the white area. The variables y0, y1, ..., y7, and z0, z1, ..., z7 denote the values of x0, x1, ..., x7 in the second and the third passes, respectively. Finally, the last intermediate value 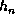is taken as the output of Tiger/192.