
תוכן
עניינים
הקדמה
תקציר
בתחום ה-Virtual Reality קיים מקום
שמור למשחקים
ויישומים
למטרות שעשוע.
עוד מאולמות
הארקייד של
שנות ה 90
המוקדמות האפשרות
שניתן ליצור
עולם שלם אשר
מגיב לתנועת המשתמש
הטבעיות בלבד
ולא בקלט
ממקלדות כבש
את ליבם של
מפתחים מכל
העולם.
הופעת מכשירי
הSmartphone-
הציגה לעולם
אפשרות שלא
הייתה קיימת
לפני. מכשיר
נייד אשר
מחזיק בתוכו
כוח עיבוד
חזק, מצלמה
וחיישני
תנועה – כל אלו
מאפשרים
יצירה של ממשק
משתמש אשר לא
תלוי בקלט
פרימיטיבי
כמו מקלדות,
אלא
הקלט הוא מעתה
עיבוד התמונה
המתקבלת
מהצלמה
וחיישני
המכשיר.
באופן זה נולד
באופן טבעי
עולם ה AR (Augmented
Reality) אשר
מתמקד ביצירת
שכבות של
גרפיקה
ולוגיקה אשר
על פיהם ניתן
לייצר עולם
שלם אשר מולבש
באופנים
שונים על גבי
העולם האמיתי
אשר נראה על המסך.
בפרויקט
זה נעשה
ניסיון לממש
מערכת משחק
דינאמית
פשוטה אשר
מאפשרת לשחקן
לייצר שלבים
ואתגרים על פי
דמיונו
והעדפותיו
האישיות.
לא עוד
שלבים
ואתגרים
המוכנים מראש
אלא מערכת
דינאמית אשר
תדע להתמודד
עם רצונות
השחקן.
בבדיקות
שנעשו בזמן
עבודת הפיתוח
ראינו כי גם
על מכשיריSmartphone
ישנים
באופן יחסי
אנו מצליחים
לקבל תוצאות
טובות אשר
עובדות בזמן
אמת.
מטרות
הפרויקט
כיום
קיימות מספר
תוכנות/מערכות
המאפשרות לשחקן
להשתמש
בשירותי
מציאות
מועשרת ((AR.
רוב המערכות
הללו בנויות
על בסיס של
מערכת המציגה
שכבות של
גרפיקה
המתחלקות ל-2
סוגים:
·
שכבות
גרפיקה
מציגות
נתונים שאינם
מושפעים ממה
שנראה על מסך –
לדוגמא ממשק
המראה את הדרך
שלפנינו
ומציג נתונים
של מהירות,
כיוון וכו'.
יש לשים
לב כי במקרה
זה השימוש
במונח AR
הינו בעייתי
שכן למרות
שאמנם הממשק
מציג שכבות של
גרפיקה
ונתונים על
המסך על גבי
התמונה
האמיתית, אין
הממשק מנתח את
התמונה,
אלא
מציג את
התמונה
המקורית ועל
גביה מציג
נתונים אשר לא
מושפעים
מהתמונה.
במילים אחרות,
אין התוכנה
מגיבה לשינוי
בתמונה (או ב Video Stream ) ושינוי של
אוריינטציית
המכשיר
לדוגמא לא תשנה
את הנראה על
המסך.
·
שכבות
גרפיקה
המסתמכות על
נתוני שרת.
במקרה זה
התוכנה אכן
מגיבה למצב
המכשיר
ומעדכנת את
הגרפיקה על בסיס
נתונים
המגיעים משרת
ייעודי. דוגמא
לכך הוא משחק Pac-man אורבני
אשר שם נקודות
ברחובות.
יש לשים
לב כי במצב זה
בזמן הליכה או
שינוי אוריינטציית
המכשיר המסך
יראה תמונה שונה,
אך יש כאן
שימוש
בנתונים
סטטיים אשר
הוגדרו על ידי
בסיס נתונים
מרכזי ואין
למשתמש אפשרות
לשנות את
האתגר שלו.
בפרויקט
זה אנו מנסים
לממש מערכת
המאפשרת לשחקן
ליצור לעצמו
בסיס לסביבת
משחק דינאמית
אשר משתנה
בהתאם לרצונו.
המטרות אשר
הצבנו לעצמנו
בתחילת
הפרויקט הם:
1. סביבה
דינמית אשר
אינה מצריכה
קבצי נתונים
(קובץ לאתגר
או קובץ
נתונים למספר
אתגרים).
2. אתגרים
המיוצרים
באופן דינאמי.
על פי תוואי השטח.
3. יכולת
אבחנה תלת
ממדית -
המערכת צריכה "לראות"
את הסביבה
ולהבין מהן
הקורדינאטות של
נקודות
העניין.
4. המערכת
היא מערכת
לאור יום בלבד
אין דרישה
לעבודה בתנאי
אור משתנים.
5. המערכת
תוכל לעבוד
באופן חלק גם
על מכשירים בעלי
חומרה כלשהי
(לא בהכרח
חומרה חזקה).
6. עבודה
מול ספרייה
אשר תנהל
עבורנו את
נושא הראייה
הממוחשבת.
7. שימוש ב OpenGL על
מנת לייצר
שכבות גרפיקה
מותאמות.
8. שימוש ב GPU של המכשיר
על מנת לייצר
גרפיקה.
על מנת
למקד את
עבודתנו
החלטנו על
סביבת משחק של
מרוץ מכוניות
ויצירת מערכת
כבישים דינמית
התלויה
בסידור של
סמנים על גבי
סביבת העבודה
ובחירות של
המשתמש לגבי
חיבורי
הצמתים (הרחבה
בהמשך).
בסיס
הפרויקט
על פי
המטרות
החלטנו לבסס
את המערכת
שלנו על מערכת
ההפעלה Android עם גרסה
2.3 ומעלה.
מערכת ההפעלה
נבחרה כיוון
שפיתוח
למערכת זאת
הינו קל וזול
(אינו דורש
תשלומים)
והסכמי רישוי
אשר מאפשרים
לעבוד במסגרת
פרויקט לימודי
ללא תשלומים
וללא חומרה
ייעודית.
בנוסף מערכת
ההפעלה Android
מאפשרת גישה
לרכיבי תוכנה
אשר מערכות
ההפעלה
האחרות בשוק (WP ,IOS) אינם
מאפשרות,
רכיבי
תוכנה אלו
כוללים אך לא
מוגבלים
לגישה פשוטה
וחופשית
לסנסורים
השונים שיש
במכשיר.
מערכת
ההפעלה Android תומכת
ב- OpenGL ES.
שימוש ב OpenGL ES
מאפשר לנו
להאיץ באופן
משמעותי את
החישובים על
ידי העברתם ל GPU של
המכשיר.
על בסיס
מערכת ההפעלה
השתמשנו
בספריית AR של
חברת QUALCOMM בשם Vuforia.
הספרייה
מאפשרת את
הדברים הבאים
עליהם אנו מבססים
את המערכת
שלנו:
1. זיהוי
של Markers
(נקודות
עניין, הרחבה
בהמשך).
2. קבלת
קורדינאטות
של כל Marker במרחב.
המערכות
שעליהם הפרויקט
נבדק ונוסה
הם:
3. Samsung Galaxy S, S4 - עם גרסת
מערכת הפעלה Android 2.3 ו- 4.0.4 Android.
4. Samsung Galaxy tab עם
גרסת מערכת
הפעלה Android 3.0.
הנחות
יסוד
כפי
שהוסבר תחת
סעיף מטרות
הפרויקט,
מטרתנו היא
לייצר בסיס
לסביבת משחק
דינמית אשר
תאפשר יצירת
אתגרים
ועדכונים
חיים
אינדיבידואלים
לאותו הרגע.
לכן
גיבשנו רשימה
של הנחות יסוד
אשר מאפשרות לנו
להקנות מסגרת
עבודה
לפרויקט:
1. סביבת
העבודה הינה
התמונה אשר
מתקבלת מהמצלמה.
2. קיימים 4
סוגי צומת
שהם:
o
צומת
T
o
מעגל
תנועה
o
צומת
L (שהוא
פנייה).
o
כביש
ישר .
ניתן
להרכיב כל סוג
של צומת על
ידי שרשור של
צמתים מסוגים
שונים.
3. מערכת
הכבישים הינה
גרף, בו
הצמתים הם
הצמתים בכביש
(אלו שהוגדרו
קודם לכן)
וקשתות הגרף
מייצגות
כבישי חיבור
בין הצמתים.
4. כל צומת
בגרף מוגדר על
ידי Marker
שזוהה בסביבת
העבודה.
5. כל קשת
בגרף מייצגת
חיבור פיסי
בין 2 צמתים.
6. אין
בגרף לולאות
עצמיות (ניתן
להוסיף לכך
תמיכה בהמשך
אך אין משמעות
נלווית
להוספת תמיכה זאת
ולכן לא
הוספה).
7. שני
צמתים יכולים
להיות
מחוברים אך
ורק על ידי
קשת אחת (גם זה
ניתן לשינוי
בעתיד).
8. הקשתות
בגרף לא
מוגדרות על
ידי נתונים
מהתמונה
ומגדרות על
ידי המשתמש
בלבד.
9. הגרף
אשר מיוצר
אינו חייב
להיות מישורי.
10. מהנחה
קודמת נובע כי
קיימת אפשרות
ששני קשתות
יחתכו אחת את
השנייה, אך
לפי הנחה 2 אין
מדובר בצומת.
במצב זה
התוכנה תדאג
למצוא את
נקודת החיבור
להתמודד עם
המצב באופן
כלשהו (הרחבה
בהמשך).
11. כביש
הינו עקומה
חלקה אשר מקיימת
![]() בכל
נקודה.
בכל
נקודה.
12. קיימת
אפשרות של
חיתוך של
כבישים במקרה
זה אנו מניחים
כי חיתוך יהיה
תמיד על מישור
XY בלבד (הנחה
זאת מקלה את
המימוש אך
אינה משנה אותו
באופן ניכר).
מערכת
הכבישים
ריכיבים
של מערכת
הכבישים
צמתים
על מנת
לייצר את
"מבוך"
הכבישים
ששמנו לעצמנו
כמטרה, עלינו
לזהות ולהציג
מספר סוגי
צמתים שהם:
5. כביש
ישר
6. צומת
o
צומת
מעגל עם 4
כניסות
(מבחינה לוגית
הדבר זהה לצומת
X)
o
צומת
T
7. פנייה
בעזרת
חלקי כביש אלו
ניתן לייצר
כמעט כל סוג של
כביש כולל
צמתים
מורכבים. אין
אנו מיחסים חשיבות
להבדל בין
פנייה ימינה
או שמאלה, שכן פנייה
ימינה היא
בעצם פנייה
שמאלה אשר
מסובבת ב ![]() .
.
על פי
המפרט של
פרויקט Vuforia
ישנם כ-500
מרקרים שונים
אשר ניתנים
לזיהוי ייחודי.
לשם נוחות
המרקרים
ממוספרים,
כאשר בתור התחלה
המספרים
המעניינים
אותנו הם:
|
|
|
|
|
מימין
לשמאל: 1. כביש
ישר, 2.. מעגל
תנועה, 3. צומת T, 4.פנייה
כל מרקר
מגדיר צומת
בגרף, ולכל
אחד מתאים
אובייקט גרפי
מאותו סוג:
|
|
|
|
|
על ידי
שימוש בחלקים
אלו ניתן
לייצר גרף של
כבישים כאשר
כל קשת בגרף
זה הינה כביש
חלק אשר יווצר
באופן דינאמי
על פי הגדרות
המשתמש.
הערה: הוספנו
שימוש בצומת
כביש ישר על
מנת לאפשר כפייה
של כביש לעבור
בנקודה
מסוימת.
על פי
המפרט של Vuforia
ניתן
בכל רגע נתון
לזהות רק מופע
אחד ויחיד של
מרקר מסוים,
כלומר אם
המצלמה קולטת
את מרקר 3
פעמיים
הספרייה של vuforia תזהה רק
את אחד מהם
(הראשון שזוהה).
כיוון
שיש 500
אפשרויות של
מרקרים ניתן
להגדיר את
המרקרים
באופן הבא:
בהינתן זיהוי
של מרקר
ומספרו ![]() הצומת
שישויך
למרקר זה הוא
הצומת
שישויך
למרקר זה הוא
![]() .
.
באופן
זה קיבלנו כ-125
אפשרויות לכל
צומת בכביש.
אשר ניתן
לראות בו זמנית.
כך שניתן
לבנות מערכת
כבישים גדולה
מאוד.
הצגה של
חלקי הכביש
ספריית
המציאות
מועשרת נותנת
עבור כל מרקר
שזוהה בהצלחה
מטריצה בגודל ![]() כאשר
כאשר
המטריצה היא
מטריצת
טרנספורמציה
הומוגנית רגילה
אשר הורדה
ממנה השורה
התחתונה ( שכן
שורה זאת היא
תמיד ![]() ) .
) .
באופן
זה אנו יכולים
לדעת את מיקום
וסיבוב הצומת
בעולם, באופן
אשר תואם את
הסיבוב של
המרקר
במציאות
ובמיקום
הנכון.
המודל
המתאים לצומת
מצויר על ידי
שימוש ב OpenGL ועל ידי
שימוש ב-Shaders אשר
נכתבו מראש.
ה-Shaders פשוטים
ואחראיים לציור
של המודל ע"י
שימוש
בטקסטורות
וחישוב של
מיקום על ידי
מטריצת העולם
והמצלמה בלבד.
כיוון
שאין אנו
מתחשבים נכון
להיום
במקורות אור
אין התחשבות
בנושא זה
ונושאי תאורה
אינם מחושבים
(אין שימוש
במשוואות
תאורה),
נושא זה
נזנח כיון
שאין לנו נכון
לרגע זה
אפשרות לזהות
מיקום של
תאורה בסצנה
על ידי שימוש
בספרית vuforia
וקביעה
ידנית/שרירותית
של מקור תיתן
תוצאות אשר
אינם תואמות
את המציאות
והדבר יראה לא
מציאותי ולא
יפה.
(המטרה
בגרפיקה היא
בסופו של יום
עניין של
מראית העין
ולכן מה שלא
נראה טוב לא
נכנס לפרוייקט).
ציור של
הצומת נעשה על
ידי הזנה של
הנקודות של
המודל לתוך הbuffers של כרטיס
המסך על ידי
שימוש OpenGL
וקריאה
לפונקציות OpenGL על מנת
לשלוח לכרטיס
המסך פקודה
לצייר את הנתונים.
המחלקה RoadPiece היא
מחלקת האב של
כל הצמתים
ומגדירה את
הפעולות
שניתן לבצע על
הצומת.
המחלקות:
8.
StraightPiece
9.
CirclePiece
10.
TPiece
11.
TurnPiece
מגדירות
את חלקי
הכביש, את
האובייקטים
הגרפיים של
חלקי הכביש
(גיאומטריה
וטקסטורות)
ואת כמות
נקודות
החיבור שלהם.
כמו כן, לכל נק'
חיבור המחלקה
מגדירה את
מיקומו,
וכיוון
הנגזרת בנק'
(לצורך בניית
כבישים מחברים,
יוסבר בהמשך).
נקודות
חיבור
נקודות
חיבור הן
נקודות על
הצומת שאליהן
יכול להתחבר
כביש חיצוני
(הנקודות
מוגדרות ע"י נקודות
חיבור טבעיות
מהמציאות). כל
סוג של צומת,
מגדיר מספר
נקודות חיבור
(כמספר
היציאות הקיימות
לאותו צומת).
לדוגמא:
לצומת T
ישנם 3 נקודות
חיבור שונות.
לכביש ישר
ישנן 2 נקודות
חיבור. כל נק'
חיבור יכולה
להיות פנויה
לחיבור כביש,
או תפוסה (אם
כביש כלשהו
כבר מחובר
לנקודה זו).
ולכל נק'
חיבור מוגדר
כיוון הנגזרת
בנק' זו.
ניתן
לראות את
נקודות
החיבור של
צומת ע"י לחיצה
על הצומת במסך
המכשיר (דוגמא
בעמוד הבא).
|
|
נקודות
החיבור
מוצגות
כנקודות
ירוקות
במקומות החיבור
האפשריים
זיהוי
לחיצה על צומת
זיהוי
לחיצות על
צומת במסך,
מתבסס על
שליחת קרן
מנקודת המגע
במסך לעולם,
ובדיקת חיתוך
בין הקרן
למסגרת
האובייקטים.
האלגוריתם:
1.
ייצר
וקטור מנקודת
המגע במסך,
ממישור
המצלמה בכיוון
התבוננות
המצלמה.
2.
לכל
אובייקט
בסצנה בצע:
2.1.
בדוק
האם הוקטור
נחתך עם מסגרת
האובייקט*
אם כן, החזר את
האובייקט.
3.
אם
לא נמצא שום
אובייקט, החזר
תשובה שלילית.
*אלגוריתם
בדיקת החיתוך
הינו
אלגוריתם Seperating Axis Theorem.
אלגוריתם זה
הינו מחוץ
לסקופ של
חוברת זו וניתן
לקרוא עליו
בהרחבה
בכתובת
הנמצאת
ב"קריאה
נוספת".
כבישים
מחברים
חיבור
של צמתים
חיבור
של צמתים (קשת)
נעשה על ידי
המשתמש. בכדי ליצור
כביש המחבר
בין 2 צמתים, על
המשתמש לעשות
את הפעולות
הבאות:
1.
לחיצה
על צומת מקור
(יופיעו על
הצומת נקודות
החיבור
האפשריות).
לחיצה נוספת
תבטל את
בחירת הצומת.

2. לחיצה
על צומת יעד
(יופיעו על
הצומת נקודות
החיבור
האפשריות).
בשלב זה יופיע
קו המתאר של
הכביש שיווצר.
לחיצה נוספת
תבטל את בחירת
הצומת.

3.
לחיצה
נוספת במקום
אחר על המסך
מאשרת את קביעת
הכביש (קשת).

אותו
סדר פעולות
בדיוק מאפשר
מחיקת כביש
(קשת) קיים.
יצירת
כביש מחבר
לכשנבחרו
2 הצמתים
להרצויים
לחיבור, מחלקת
מנהל הכבישים
(תתואר בהמשך),
תבדוק האם
לשניהם קיימות
נק' חיבור
זמינות. במידה
ולא קיימות
נק' חיבור
זמינות, יצירת
הכביש לא
תתאפשר.
מתוך כל נק'
החיבור, יבחר
מנהל הכבישים
נק' מכל צומת,
כך שהמרחק
האוקלידי בין
הנק' הוא הקטן
ביותר האפשרי,
ייצור קשת בין
2 הצמתים
הנתונים
וישמור את
הקשת במבנה
הנתונים.
האלגוריתם:
1.
בדוק
האם לצומת
היעד וצומת
המקור קיימות
נקודות חיבור
פנויות. אם לא,
בטל את יצירת
הכביש
2.
אפס
מרחק מינימלי
לMAX_FLOAT-
3.
עבור
כל נקודה פנויה
בצומת המקור
בצע:
3.1.
עבור
כל נקודה
פנויה בצומת היעד
בצע:
3.1.1. בדוק
האם המרחק
האוקלידי קטן
מהמינימלי. אם
כן, שמור את
המרחק
המינימלי
החדש ואת נק'
המקור והיעד
4.
צור
קשת מנק' היעד
והמקור בעלות
המרחק המינימלי,
ואחסן אותה
במבנה
הנתונים.
אובייקט
כביש מחבר
(קשת)
קשת
הינה אובייקט
לוגי והיא
מוגדרת על ידי
המחלקה RoadConnector.
המחלקה
אחראית על
שמירת צמתי
המקור והיעד
ונק' החיבור
הרלוונטיות.
כמו כן, בניה
מחדש של
גיאומטריית
הכביש המחבר בכל
פריים של
המצלמה.
(מסלול הקשת
אינו מחושב במעמד
יצירת
האובייקט אלא
היא מחושבת
מחדש בכל פריים,
שכן
אובייקטים
זזים כל הזמן,
לפחות בפוטנציאל,
ומערכת
הכבישים שלנו
דינמית ומתעדכנת
בזמן אמת). כמו
כן, המחלקה
אחראית על
ציור הכביש
המחבר על
המסך.
בניית
גיאומטרית
הכביש
בסיס כל
גיאומטריית
הקשת הינו Cubic
Hermit Spline
היוצא מנק'
חיבור היעד,
לנק' חיבור המקור.
כיוון
הנגזרות בכל
נק' חיבור
מוגדר ע"י מחלקת
הצומת
המתאימה.
גודל הנגזרת
ניתן לשליטה
ע"י ממשק
המשתמש. בצורה
זו, הכביש
נראה טבעי.
בניגוד לכביש
פרבולי או
לינארי שלרוב
אינו קיים
במציאות. כמות
נק' הדגימה של
העקומה, ניתנת
לשליטה ע"י
ממשק המשתמש.
לאחר
שנוצה עקומת
הבסיס, נחשב
את שאר
הגיאומטריה
בצורה הבאה:
1. עבור כל 3
נקודות
סמוכות על
העקומה נבצע:
1.1. בנה
מלבן מסביב
לכל 2 נקודות
סמוכות, כאשר
ציריו הם
וקטור הישר
בין 2 הנק',
והוקטור
הניצב לוקטור
זה. ורוחבו
קבוע (כרוחב
הכביש הרצוי).
(אילוסטרציה
בעמוד הבא)
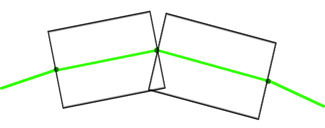
1.2. חבר את את 2 זוגות
הנקודות
מהצדדים
הקרובים של
המלבנים בקו.

1.3. בחר את
נקודת האמצע
בכל אחד
מהקוים הנ"ל,
להיות נקודה
בגיאומטריה
של הכביש.

2. לאחר
קבלת כל
הנקודות
בצורה הנ"ל,
נשלש את הגיאומטריה
בצורה הבאה:

בנוסף
עלינו לוודא
כי הנק'
המתחברות
לאובייקטי
הצמתים,
יושבות בדיוק
על הצמתים.
בעזרת
תהליך זה, אנו
יוצרים את 2
המשטחים, העליון
והתחתון, של
הכביש לפי
הגבהים של
גיאומטריית
אובייקטי
הצומת. לאחר
שאלו קיימים,
ניתן לחבר את
הנקודות של
העליון
והתחתון, ע"י
שילוש זהה
לנ"ל.
נשים לב,
שבתהליך זה,
ככל שמספר
נקודות
הדגימה גבוה
יותר, נקבל
כביש הקרוב
יותר לצורת
עקומת הבסיס
(מניסויים
שביצענו,
גילינו שמספר
די קטן של
נקודות דגימה,
כבר מספיק
בכדי שהכביש
יראה טוב
מאוד. תכונה זאת
חשובה, מכיוון
שאנו מבצעים
את כל הבניה
הזאת מחדש בכל
פריים של
המצלמה. ולכן,
ככל שנצטרך פחות
נקודות, כך
החישוב יהיה מהיר
יותר ולא
ישפיע על
חווית
המשתמש).
כביש הנוצר
מעקומה בעלת 5
נק' (מימין) מול
כביש הנוצר
מעקומה בעלת 25
נק' (משמאל).
יצירת
קואורדינטות
הטקסטורה על
הגיאומטריה
מתבססת על כך
שהטקסטורה
מחזורית וכמו
כן, התמונה
ההפוכה (מהסוף
להתחלה) היא
זהה.
|
|
|

לכן גם קואורדינטות הUV- הן מחזוריות ועוברות על התמונה הלוך וחזור:

כך
נוצרת תמונה
חלקה
ומחזורית,
הנראית טוב לאורך
כל הכביש. על
צדי הכביש אנו
משתמשים
בטקסטורה
שונה (הנראית
כמו אבנים), אך
באותו עקרון בדיוק.

ניהול
הכבישים
וריצה שותפת
מנהל
הכבישים
מחלקת מנהל
הכבישים
מנהל
הכבישים
מיוצג ע"י
המחלקה RoadManager. מחלקה
זאת אחראית על
ארגון כל חלקי
הכביש (צמתים
וכבישים
מחברים),
יצירת ושמירת
הקשרים ביניהם,
וציורם על
המסך.
האפליקציה
מכירה
ומתקשרת אך
ורק עם מחלקה
זו, והמחלקה
אחראית על כל
שאר העבודה.
ריצה
שותפת של האפליקציה
תחילה
מנהל הכבישים,
מאתחל את מבנה
הנותונים בכל
המרקרים
הניתנים
לזיהוי. תהליך
זה קורה פעם
אחת, וכל
המקומות
המשתמשים
בצמתים,
משתמשים
במופעים אלו
של הצמתים.
כאשר
מגיע פריים
מהמצלמה,
האפליקציה
פונה למנהל
הכבישים
ומעבירה לו את
מטריצת ההטלה
של המצלמה. כאשר
בתורו מנהל
הכבישים מבצע
את הפעולות
הבאות:
1. עבור כל
מרקר מזוהה
(מנוהל על ידי
ספריית Vuforia)
1.1. שלוף את
המרקר ממבנה
הנתונים
(מזוהה ע"י
אינדקס
המרקר).
1.2. עדכן את
המטריצת ה-ModelView של ה-RoadPiece הרלוונטי
לזאת שנמצאה
על ידי
הספרייה.
1.3.
צייר
את האובייקט
בעזרת OpenGL
והמטריצות
שנמצאו.
2. עבור כל
כביש מחבר
קיים בין
צמתים ( קשת )
2.1. שלוף
צומת מקור
2.2. שלוף
צומת יעד
2.3. העבר את
מטריצת ה-ModelView של
צומת יעד
לעולם של של
צומת המקור.
מתבצע תרגום
של מודל היעד
לעולם של מודל
המקור, בכדי שכל
הכביש יהיה
באותו העולם.
3. עבור כל
זוג כבישים
מחברים בצע:
3.1.
בדוק
האם ההטלה של
הכביש השני על
הכביש הראשון,
יוצרת חתוך
(הרחבה בהמשך).
אם כן, סמן
כביש מחבר זה.
4.
עבור
כל כביש מחבר
בצע:
4.1. בנה את
גיאומטריית
הכביש המחבר,
עפ"י כל המידע
הנאסף לפני.
(אם הכביש
מסומן הרם את
הכביש בנקודת
החיתוך).
4.2. צייר את
גיאומטריית
הכביש בעזרת OpenGL וכל המידע
הנאסף לפני.
כמו כן,
במהלך ריצת
האפליקציה,
יכולים
"להדחף"
הוראות
מהשכבת ממשק
המשתמש,
הוראות אלה
עלולות לשנות
את הפרמטרים
השונים
באפליקציה. גם
שינויים אלה
מתבצעים ע"י
פניה למנהל
הכבישים.
חיתוך
עקומות
כפי
שהוסבר קודם
לכן, קיים
צורך לדעת האם
שתי עקומות
כלשהן אכן
נחתכות, ואם
כן מהי נקודות
חיתוך שלהם.
הפתרון
הנאיבי של
בעיה זאת היא
חיפוש נקודת
חיתוך על ידי
השוואת
משוואות
העקומים בתקווה
למצוא נקודת
חיתוך.
עם זאת,
גישה זאת אינה
אפשרית בפועל
כיוון שלרוב
העקומות
(ובפרט עקום
הרמיט) יש
מעלה הגדולה מ
2 ואין נוסחא
הנותנת פתרון
למשוואות מסדר
זה.
(יש
נוסחא סגורה
לפתרון
משוואות ממעלה
3 אך פתרון זה
מסובך ועלול
לתת 3 תוצאות
ואז יהיה צורך
לבדוק מי
מתוצאות אלה
אכן התוצאה
שאנו מחפשים).
כמו כן,
העקומות
מייצגות
גיאומטריה התופסת
איזור גדול
יותר במרחב,
ולכן חיתוך של
שני הכבישים
המלאים, עלול
להתבטא בקלות
בחוסר חיתוך
בעקומות
המייצגות
אותם.
מכיוון
שאנו
מעוניינים
לקבל קירוב
לנקודת החיתוך
ואין לנו צורך
בנקודת חיתוך
מדוייקת, ניתן
לחפש דרכים
לקירוב
התוצאה אם
נטיל את העקומות
על "רצפת"
העולם של
העקומה
הראשונה.
כעת אנו
מתעסקים
בעקומת דו
ממדיות.
כיוון
שאנו עובדים
עם עקום באופן
דיסקרטי (אוסף
של נקודות)
ניתן לחפש את
נקודת החיתוך
המשוערת.
נשים כי מאופי
העקומות
שאיתן אנו
מתעסקים ומאופי
נקודות
החיתוך, נוכל
להניח כי אנו
מתעסקים עם
עקומות שלהן
יהיו לכל
היותר נקודת
חיתוך אחת ויחידה:
|
|
|
המצב
מימין, אפשרי
אך המצב משמאל
לא אפשרי (אם אפשרי,
אז נדיר מספיק
בשביל שנתעלם
ממנו).
ניתן
לראות בקלות
כי במקרים
שאנו מחפשים
לרוב(אך לא
בהכרח) אם
קיים חיתוך של
העקומות יהיה חיתוך
של הישרים
המקשרים בין
נקודות הקצה
של הישרים.

אמנם
קיימים מקרי
קיצון שבהם
מצב זה לא
מתקיים
לדוגמא:

ניתן
להגדיר סט
תנאים אשר
מכריחים את
החיתוך של
הישרים להיות
מהצורה
הראשונה.
תנאים אלו כוללים
בין היתר אורך
העקומות
והמצב ההדדי
בניהם. אנו
נניח שמצב זה
אכן מתקיים
ונתבונן במה
שקורה במידה
ומצב זה אכן
קיים.
במידה
ונתונות לנו 2
עקומות אשר
נחתכות,
והישרים
המחברים את
נקודות
הקיצון אכן
נחתכים אזי
עובדה זאת נשארת
נכונה גם בתתי
חלקים של
העקום.
לדוגמא
אם נחלק כל
עקום ל2 נוכל
למצוא את אותו
האפקט.

ניתן
לראות כי בשני
העקומות
החלקים
השמאליים של
העקומות
נחתכים וכך גם
הישרים המחברים
בין קצוות
העקום.
נוכל
להשתמש
בעובדה זאת
ולחפש קירוב
ליניארי תוך
על ידי חיפוש
ישרים קטנים
יותר ויותר אשר
נחתכים וכאשר
נגיע לגבול
(הדיסקרטי) של
העקום נחזיר
את הקירוב
הנתון.
בהינתן 2
ישרים אשר
עוברים
בנקודות
1. ישר 1![]()
2. ישר 2 ![]()
נקבל את
קורדינטת x של
נקודת החיתוך
על ידי הנוסחא

נקבל את
קורדינטת y של
נקודת החיתוך
על ידי הנוסחא

נשים לב
כי לא קיים
חיתוך בקטע
אזי נקבל
חלוקה באפס
כלומר במובני
שפת תכנות NaN.
נקודה
זאת חשובה
כיוון שכך
ניתן בקלות
לדעת האם 2
קטעים נחתכים
– על ידי חישוב
הערך ובדיקה האם
הערך הוא NaN.
באופן
זה ניתן לייצר
מעין חיפוש
בינארי אשר מחפש
קירוב לנקודת
החיתוך, זאת
על ידי בדיקה
האם קיימת
נקודת חיתוך
בין הקטעים
במידה וכן, חלוקה
של הקטע ל-2 ובדיקה
זהה על תתי
החלקים.
נתבונן
באלגוריתם
הרקורסיבי
הבא:
קלט:
מערך של
נקודות
המייצגות את
העקום a
ומערך המייצג
את העקום b.
פלט:
קביעה האם
קיים חיתוך
בין העקומים
ואם כן נקודת
חיתוך משוערת.
1. בדוק
האם קיים
חיתוך בין
הישרים
הנוצרים על ידי
נקודות הקצה
של עקום a ונקודות
הקצה של עקום b.
2. במידה
ולא החזר שקר.
3. אם
ועקום a
מיוצג על ידי 2
נקודות בלבד
ועקום b
מיוצג על ידי 2
נקודות בלבד
a. החזר את
נקודת החיתוך
בין 4 נקודות
הנתונות
b. אחרת
i.
אם
עקום a
ניוצג על ידי
יותר מ2
נקודות חלק את
עקום a
לשניים ![]() .
.
ii.
אם
עקום b
ניוצג על ידי
יותר מ2
נקודות חלק את
עקום b
לשניים ![]() .
.
iii.
חזור
ל 1 עם הערכים ![]()
iv.
חזור
ל 1 עם הערכים ![]()
v.
חזור
ל 1 עם הערכים ![]()
vi.
חזור
ל 1 עם הערכים ![]()
קיבלנו
אלגוריתם
רקורסיבי אשר
מחזיר לנו קביעה
האם קיימת
נקודת חיתוך
ואם כן היכן
היא.
לא נציג
הוכחה מסודרת
הנהוגה בקורס
אלגוריתמים
זאת כיוון
שכפי שהצגנו
קודם לכן
יתכנו מצבים
שבהם אכן קיים
חיתוך בין
עקומות אך
האלגוריתם לא
ימצא זאת.
להלן
דוגמא לריצת האלגוריתם
מימין לשמאל:

|
|
|
|
קיבלנו
את הנקודה
הכחולה. וזהו
קירוב טוב לנקודת
החיתוך.
הרמת
עקומה
כאשר
זוהה חיתוך של
עקומות הדבר
אומר ששני כבישים(קשתות)
חותכים אחד את
השני ללא
צומת.
על פי לוגיקת
הגרף כיוון
שאין צומת
המחבר את הכבישים
אזי אין
אפשרות לעבור
מקשת אחת
לשנייה כלומר
יש לפתור את
העניין באופן
גרפי אשר יהיה
תואם ללוגיקת
הגרף.
הפתרון
שבחרנו הוא
לבצע אפקט של
הרמה לאחד הכבישים.
אפקט ההרמה
מתבצע על ידי
הוספת גובה לעקומה
באופן שיאפשר
לאחת העקומות
לעבור מעל השנייה.
על פי
ההנחה כי
חיתוך מתאפשר
על מישור XY אנו
יודעים כי
תמיד יש
להוסיף גובה
רק בציר אחד
ויחיד שהוא
ציר הגובה.
על פי
ניסיונות
שונים ראינו
כי אנו מקבלים
תוצאות
משכנעות על
ידי שימוש
בפונקציה
גאוס כאשר
מרכז
"הפעמון" הוא
בנקודת
החיתוך. עקומה
זו נראית הכי
טבעית ולא
מאולצת.
העקומה מקבלת
גובה (בציר Y)
בתלות במרחק
מנקודת
החיתוך. נוסחת
גאוס נתונה על
ידי:
![]()
במקרה
שלנו ![]() הוא
המיקום של
נקודת החיתוך.
בכך אנו יוצרים
תלות הפוכה
במרחק בין
הנקודה
הנוכחית לנקודת
החיתוך.
הוא
המיקום של
נקודת החיתוך.
בכך אנו יוצרים
תלות הפוכה
במרחק בין
הנקודה
הנוכחית לנקודת
החיתוך. ![]()
ואילו ![]() הוא פרמטר
המאתר את רוחב
העקומה. פרמטר
זה הוא פרמטר
אשר אינו קשור
באופן כלשהו
לעקומה או
לעולם כלשהו
אלא פרמטר אשר
ייתן עקומה
אשר תראה טוב.
הוא פרמטר
המאתר את רוחב
העקומה. פרמטר
זה הוא פרמטר
אשר אינו קשור
באופן כלשהו
לעקומה או
לעולם כלשהו
אלא פרמטר אשר
ייתן עקומה
אשר תראה טוב.
פרמטר
זה ניתן
לשינוי ע"י
ממשק המשתמש.
סיכום
מילות
סיום
לאחר
סיום
הפרוייקט,
נוכל לומר כי
המטרות שהצבנו
לפרוייקט זה
הושגו. בנינו
תשתית טובה
לבניית
אפליקציה
התומכת בקוסטומיזציה
של מפת המשחק
ע"י המשתמש
ופותחת פתח
להרבה
אפשרויות
מעניינות
בעתיד.
כמו כן,
הצורה בה
האפליקציה
בנויה, מאפשר
פיתוח של
הפלטפורמה
ההתחלתית
בקלות. לדוגמא,
מאוד פשוט
להוסיף עוד
סוגי צמתים
וכו'. בנוסף,
כמו בכל מה
שקשור
לגרפיקה, זה
בונוס ענקי
שהכל גם נראה
יפה.
למדנו
הרבה על לעבוד
בסביבה של זמן
אמת, וכמה הסביבה
הזאת שונה
מסביבה סטטית,
כמה חשובה היעילות
ואיך כל בעיה
קטנה בקוד
עלולה להשפיע
בצורה מיידית
ומהירה על
התוצאה
הסופית.
אפשרויות
המשך
לפרוייקט
ניתן
להמשיך פרוייקט
זה בכמה
כיוונים
שונים:
1.
לקחת
את הפרוייקט
כפלטפורמה,
ולבנות משחק
על גביו,
הנותן שליטה
במכונית
הנוסעת על
מערכת הכבישים
לדוגמה.
2.
להוסיף
לתשתית תמיכה
באובייקטיבים
מבוססים
מיקום כלשהם,
בכדי לאפשר
יצירת מטרות
משחק ע"י
המשתמש (אולי
גם ע"י
מרקרים).
3.
להמשיך
לפתח את
הפלטפורמה,
לדוגמא, הוספת
בניית גיאומטריה
אוטומטית
כגון עמודים
לגשרים הוספת
סוגי צמתים
שונים ועוד.
4.
השמיים
הם הגבול!
קריאה
נוספת
Qualcomm Vuforia:
http://www.qualcomm.com/solutions/augmented-reality
Separating Axis Theorem:
Cubic Hermite Spline:















