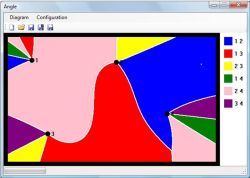
Goal: 1-point & 2-point Site Voronoi Diagrams
s project gives an easy interface for creating and editing Voronoi Diagrams. The user can create diagrams of 1-point sites or 2-point sites. In addition, the user can edit the sites and the chosen distance function. The application comes with 14 built-in distance functions.
In addition to the expected interface for the creation and editing of the diagrams, our application offers the unique feature of allowing the user to create additional distance functions. This is done within the application and so the functions are compiled on-the-fly and can be used immediately.
All the data can be saved and loaded from files. Images of the diagram and of its legend can also be saved to files.
General Functionality
Diagrams
A Voronoi Diagram can be created and edited later. A diagram holds the following data:
- Size - The size of the diagram by width and height.
- Compute-by - Whether the diagram is a nearest-neighbor or a furthest-neighbor diagram. The nearest neighbor is the site that is nearest to the current point calculated by the distance function, while the furthest neighbor is the site that is the furthest accordingly.
- Site-mode - The number of points per site. The available options are 1 and 2.
- Distance function - The function by which the diagram is computed. The function can be chosen from the list of existing functions according to the chosen site-mode. As mentioned above, the user can add his or her own functions, which will automatically be added to this list. Each diagram can be saved and loaded from a file separately. In addition, the image of the diagram and of the legend (color table) of the sites can be saved in an image file.
- Name - The name (character string) of the point. It can be any string chosen by the user, but when a point is added through a context menu, it receives a sequential number-the next unused number.
- Location - The location (x,y coordinates) of the point in the diagram. The origin ((0,0)) is the bottom-left corner of the diagram, and each location is represented by a pixel in the display.
- Color (1-point site) or Colors (2-point site) - When the site-mode is 1, the point itself is a site and it only needs one color to represent its regions. On the other hand, when the site-mode is 2, each point creates a site with each other point. In this case each point is associated with several colors - one for site it is part of.
- Abilities - The user can add, edit, duplicate, and remove distance functions.
- Template - All distance functions have to be implemented by the same template that the application enforces. This makes it very easy for the user to add a new function since all he or she has to do is to code the computation of the distance function and to add some minor data such as the name of the function.
- omposition - Composition of distance functions is essentially built-in, since and (programming language) function can call any other function. Needless to say, avoiding infinite recursive calls and calling loops are the responsibility of the user.
- Help Functions - The user can add help functions that can be called from the distance functions. This can save time and bugs of code repetition. These functions are entered in a free form.
- Debug Abilities - The application allows the user to check the results of the function on the diagram display.
- Built-in Functions - The application comes with 14 built-in distance functions which are described below.
- General Parameter - The application has a general parameter for calculating the norm between two points, also known as the p-norm. All the function calculations depend on this parameter. The default value is naturally 2, since the regular Euclidian distance is the 2-norm.
- 1. p-Norm - The p-norm defining the distance between a site and a point according to the general parameter.
- 2. Sum of Distances - The sum of distances between each point of the site and the current point.
- 3. Triangle Area - The area of the triangle defined by the two points of the site and the current point.
- 4. Distance from A Line - The (orthogonal) distance between the line defined by the two points of the site and the current point.
- 5. Distance from A Segment - The (shortest) distance between the line segment defined by the two points of the site and the current point.
- 6. Difference between Distances - The absolute value of the difference between the distances between each point of the site and the current point.
- 7. Triangle Perimeter - The perimeter of the triangle defined by the two points of the site and the current point.
- 8. Circle Radius - The radius of the circle defined by the three points (two points of the site and the current point).
- 9. Containing Circle Radius - The radius of the minimum circle which contains all the three points (two points of the site and the current point).
- 10. Angle - The smallest angle created by one of the points of the site, the current point, and the other point of the site.
- 11. Inscribed Circle Radius - The radius of the circle inscribed in the triangle defined by the three points (two points of the site and the current point).
- 12. Distance between a Segment and the Circle Center - The (shortest) distance between the line segment defined by the two points of the site and the center of the circle created by the three points (two points of the site and the current point).
- 13. Triangle Area with the Circle Center - The area of the triangle defined by the two points of the site and the center of the circle defined by the three points (two points of the site and the current point).
- 14. Triangle Perimeter with the Circle Center - The perimeter of the triangle defined by the two points of the site and the center of the circle defined by the three points (two points of the site and the current point).
- [1] A. Okabe, B. Boots, and K. Sugihara, Spatial Tessellations: Concepts and Applications of Voronoi Diagrams, Wiley, New York, 1992.
- [2] G. Barequet, M.T. Dickerson, and R.L.S. Drysdale, 2-point site Voronoi diagrams, Discrete Applied Mathematics, 122 (2002), 37-54.

Here are a few diagrams produced by the application (using the legend above):

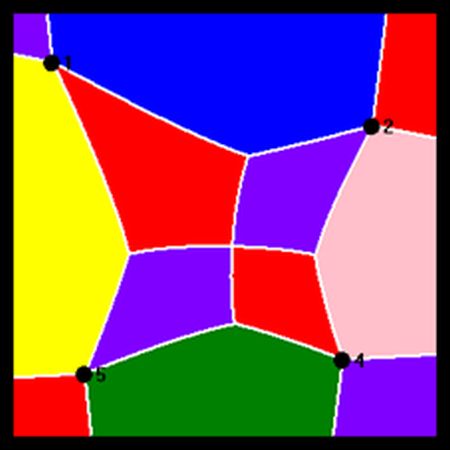
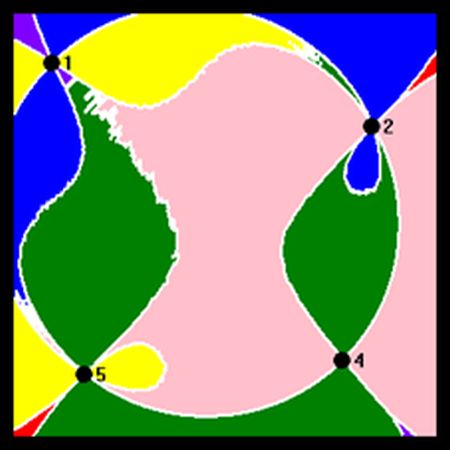
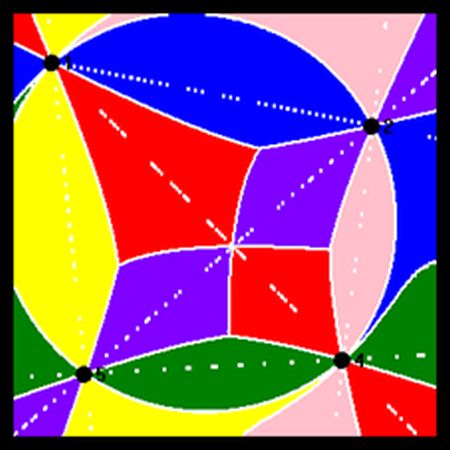
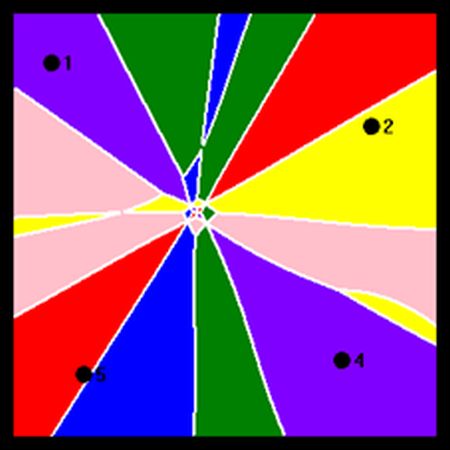
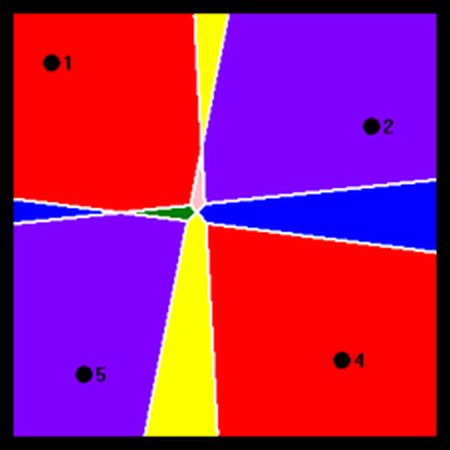
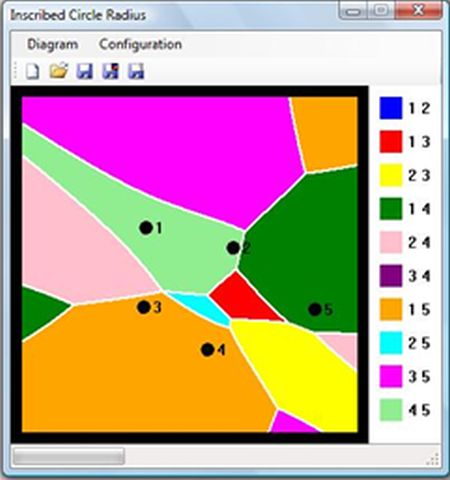
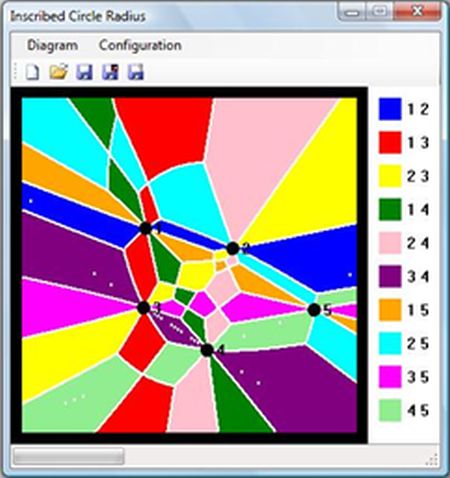
Display
The diagram is the main feature of the main window. It is drawn with all of its points (sites) and with a frame. Each site has its own color in the diagram, that is, each region of the site is drawn with the color chosen for the site. All sites and their colors are displayed in a legend table on the right side of the diagram. The display of the legend can be changed through the configuration file or menus.
Diagram Computation
Our approach to computing the diagrams is pixel-wise, that is, for each pixel we compute its distances from all sites, and color the pixel by the color of the nearest or furthest site (consisting of either one or two points). The computation of the diagram is very time consuming since it requires O(nm) time, where n is the number of pixels in the diagram, and m is the number of sites. Notice that p denotes the number of points in the diagram, then m=p in the case of 1-point sites, but in the case of 2-point site we have m=?(p^2 ). For this reason, all the distance calculations are performed on programming-language primitives (e.g., integer and double variables), whereas objects (e.g., points) are not used.
Due to the performance issues mentioned above, the diagram is recomputed only when necessary. Such times include situations in which a point is moved, deleted, or when a general parameter is modified (see the section on Distance Functions). The only time a partial computation is performed is when a new point is added to the diagram. In this case, only the distances of the new sites (in 2-points sites there are many new sites in such a situation) to each point are calculated and checked for the smallest/largest from points in the plane (as opposed to the full computation, which calculates and checks all sites).
Changes to the diagram which affect only the display but not the computation of the diagram do not result in recomputing the diagram. These include, for example, a change in a color, in particular sites' colors, the boundary width, etc. The first will only cause a redraw operation, while the second will cause some minor calculations that do not affect the main computation at all.
There exist two features of the interface which intend to help the user on this issue. The first feature is a progress bar which shows the progress of the computation. The second feature is a "freeze mode" which the user can enable at any time. While being in the freeze mode, no computation is made and the computation bar becomes blank. (The points, frame, and legend are still displayed). When disabling the freeze mode, a full recomputation of the diagram is carried out, and the diagram is, of course, redrawn on screen. This feature allows the user to make many changes at once without waiting for the recomputation of the diagram after each change.
Numerical analysis also has to be taken into consideration when coding the functions, so that the calculations of extremely small (or large) numbers will produce the correct result in a consistent manner, so that the program will always be able to compare distances reliably. This is also true for infinite distances (which are certainly possible under some definitions of distances), where the program needs to decide "which infinite is larger." Comparing infinite numbers was implemented to be sensible to the logical meaning of the distances. For example, when calculating Triangle Area with the Circle Center, in case the circle has an infinite size (which happens the three points, the considered point and the two points defining the site) are collinear (lying on the same line), two infinite quantities are compared by comparing the length of the base of the triangle, which is the distance between the two points of the site. In many cases, such "topological comparison" provides the desired comparison between infinitesimally-small, very large, or even infinite measures.
Sites
After the diagram is defined, the user may add points to it. The points can be added, edited, or deleted, using the suitable form. In addition, points can be added, moved, and deleted directly from the display through a context menu (a mouse right-click menu). Each point holds the following data:
Distance Functions
This is the most important part of the application. Since this degree of freedom is one of the most important issues in the research of Voronoi Diagrams, the flexibility offered by this project makes the analysis of diagrams much easier, especially for functions that are not intuitive, such as Circle Radius. These distance functions are the bottleneck of the diagram computation and so special care was taken while designing the implementation of the computation of complex distance functions. The program offers the following features for editing distance functions:
Built-in functions
1-point site
2-point site
Configuration
The application allows the user to change the display parameters, such as frame or boundary color and size. In addition, the user can change some of the defaults for certain forms.
Configuration Hierarchy
Changes to the configuration are made hierarchically. This way, a change can be made on the diagram level or on the application level, as the user prefers. For each datum in the configuration, the application chooses the lowest level of change. This means that if a change was made on the diagram level, it will be chosen first, then on the entire application level, and finally the default value given by the application. The configuration on the diagram level is saved within the diagram file, so that it can be loaded and used later. The configuration on the application is saved in a general file which is loaded automatically when the application starts.