| Eli Biham, Alex Biryukov, Orr Dunkelman, Eran Richardson | Adi Shamir | ||
| Computer Science Dept. | Applied Math Dept. | ||
| Technion | The Weizmann Institute | ||
| Israel | Israel |
In a note from June 25th, we described our initial observations on SkipJack, after several hours of analysis. In this note we summarize our new observations after several days of analysis.
The main new result in this note is an attack on a variant of SkipJack which contains all 32 rounds but omits four XORs. We call this variant SkipJack-4XOR (SkipJack minus four XORs). For the sake of simplicity, we describe in this note an unoptimized attack which requires 2^48 time, using about 2^25 chosen plaintexts or about 2^49 known plaintexts. Improved attacks on SkipJack-4XOR and on other variants which are even closer to SkipJack will be described in a forthcoming note.
This is still a preliminary result, but it reiterates our earlier comment that SkipJack does not have a conservative design with a large margin of safety.
In the remainder of this note we first describe additional observations and extensions of our previous note, and then describe a new technical tool, which we call the Yoyo game. Finally, we describe a simple version of our attack on SkipJack-4XOR, which suffices to get the above results.
We had also investigated other differentials of G. The characteristics we described with probability of around 2^-10.42 (and other lower probability characteristics with zero differences in the first and fourth rounds of the G permutation) do not have any counterparts, and thus the corresponding differentials have the same probabilities as the characteristics. The best other differential we are aware of is 002A->0095 with probability 2^-14.715, and the best possible differential with the same input and output differences is 7F7F->7F7F with probability 2^-15.84.
David Wagner (private communication) described various interesting improvements and provided an extended attack on the 16-round variant of SkipJack. We are grateful for his insightful contribution.
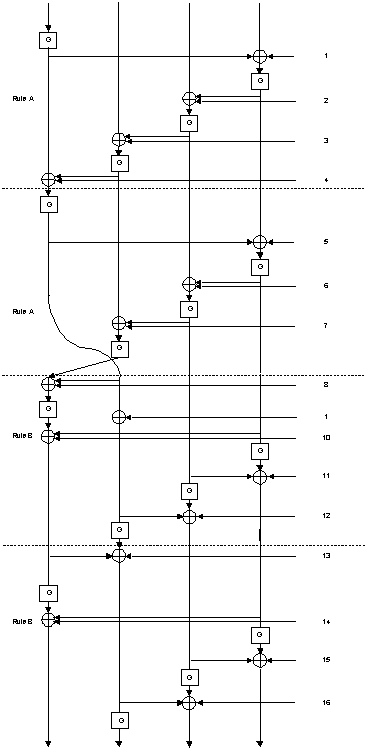
A better presentation of the first 16 rounds of SkipJack than the one presented in our previous note is:

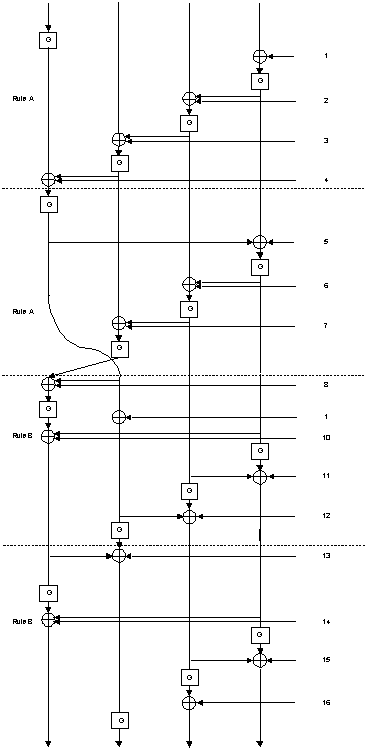
We next observe that given a pair with such an equality in the data, we can exchange the first word of the plaintexts (w^*_1, w_2, w_3, w_4) and (w_1, w^*_2, w^*_3, w^*_4), and this new pair of plaintexts still has the same property of equality in the input of round 5. Moreover, if the first words of the plaintexts are equal (i.e., w_1=w^*_1 and thus exchanging them does nothing) we can exchange the second words (w_2 with w^*_2) and get the same property. If they are also equal, we can exchange w_3 with w^*_3 and get the same property. If they are also equal, we exchange w_4 with w_4^*. However, if the property holds, this last case is impossible, as a difference of only one word ensures that the property is not satisfied.
Given the ciphertexts we can carry out a similar operation of exchanging words 2. If words 2 are equal, exchange words 1, then words 4, and then words 3. Also in this case a difference of only one word ensures that the property is not satisfied.
The Yoyo game starts by choosing an arbitrary pair of distinct plaintexts P_0, P^*_0. Both plaintexts are encrypted to C_0, C^*_0. We exchange a pair of words of the two ciphertexts as described above, receiving C_1 and C^*_1, and decrypt them to get P_1, P^*_1. Now we exchange the words of the plaintexts as described above, receiving P_2 and P^*_2, and encrypt to get C_2, C^*_2. The Yoyo game repeats this forever.
In this game, whenever we start with a pair of plaintexts with equality at the leftmost word in the input of round 5, all the later received pairs of encryptions must have the same property, and if we start with a pair of plaintexts which have different values at the leftmost word in the input of round 5, all the later received encryptions cannot have equality in any of the subsequent pairs of encryptions.
There are some heuristic techniques to identify that a cycle of such pairs of encryptions does not have the equality property. For example, when we receive a pair of plaintexts (or ciphertexts) of which three words are equal but the fourth differ, we know for sure that the equality property does not hold, and thus all the pairs in the cycle do not have such an equality. As there are four cases for such 48-bit zero differences, the probability of obtaining such pairs is 2^-46 in each step of the game. Once such a pair is encountered, we can stop the Yoyo game, since we know that its continuation will simply repeat the same sequence of steps in reverse order.
On the other hand, if the equality property holds we are ensured that at least two words differ, and thus each step generates a new set of encryptions. As the whole process is reversible, the expected cycle size is proportional to the number of such pairs, i.e., O(2^112).
This game can be used for several purposes. The first is to identify pairs with the equality property. After trying 2^16 pairs, and computing the game for each, we can identify the few with a cycle of size larger than 2^50 for instance. (Note that it is easy to generate 2^16 pairs from 2^16+1 plaintexts in such a way that exactly one of them satisfies the property). Then we can use it to recover the keys. However, as we are aware of better attacks on the same cipher, this is not proposed here.
Another application might be to increase the probability of finding right pairs for other attacks. Assume that we already got a right pair, and wish to compute additional right pairs. If right pairs have the same equality property, then such a game can give us many candidates with this property for almost free.
The starting point of the attack is the observation that the differential characteristic we used in our previous note can use partially unspecified differences. In this way we can use the following characteristic of SkipJack-4XOR: An initial unspecified difference (a,b,0,0) leads to the difference (0,c,0,0) with probability 2^-16 for some non-zero a,b,c. This difference leads to some difference (d,0,0,0) in the data (as represented in the above figure) between rounds 8 and 9, and to some (e,0,0,0) after round 12. The difference after round 16 becomes (f,g,0,0) for some non-zero f and g. This 16-round characteristic has probability 2^-16. It is easy to see that this characteristic is iterative, and thus a full 32-round characteristic of SkipJack-4XOR has probability 2^-32.
Given 2^32 pairs of plaintexts differing only in the leftmost two words, and their ciphertexts, it is easy to discard almost all the wrong pairs, as the ciphertext pairs should have the same values of the rightmost two words. Thus it is expected that only one right pair remains, along with one wrong pair. Due to their simple characterization, these 2^32 pairs can be packed into a single structure of 2^17 chosen plaintexts, or alternatively be found in approximately 2^33 known plaintexts.
The actual attack requires four distinct plaintexts (rather than a pair) with the same value of the rightmost two words, and which happen to have the same value v_1 of the leftmost word in the input of round 5, and the same value v_2 of the leftmost word in the input of round 21 (for some arbitrary v_1 and v_2). Such four plaintexts are expected to be found in a structure of 2^25 random plaintexts whose rightmost two words are fixed, as the number of quartets is about 2^96, and there are six 16-bit equality conditions at rounds 5 and 21. Given the ciphertexts, it is easy to identify the right pairs, and thus also the four plaintexts and their corresponding ciphertexts. Now, we know that the data in the second word after round 28 is the same in all four encryptions. Notice that the G permutation in round 32 and the G permutation in round 29 share two common key bytes.
For the four ciphertexts, try decrypting the second word by all the possible 32-bit subkeys of round 32 (i.e., defined by the key bytes cv_4, ..., cv_7), receiving some values X1,X2,X3,X4 for each possible subkey. Keep the differences X1 XOR X2, X1 XOR X3, X1 XOR X4 in a table together with their corresponding subkeys cv_4, ..., cv_7. We also know the outputs of the G permutation in round 29 up to some unknown 16-bit fixed value (which is the common value of the rightmost word at that round), and we know that the inputs Y1,Y2,Y3,Y4 satisfy (Y1 XOR Y2, Y1 XOR Y3, Y1 XOR Y4) equal the 48 bits in the real (X1 XOR X2, X1 XOR X3, X1 XOR X4). We can try all the 2^48 possible combinations of the 16-bit fixed value and the 32-bit subkey of round 29, consisting of cv_6,...,cv_9, and compute the 48-bit differences. For each such value we verify that such a difference exists in the table and that the common two key bytes are equal. It is expected that about 2^16 possible candidate combinations of the fixed value, of the 32-bit subkey of round 29, and of the subkey of round 32 remain. Thus, we get 2^16 candidates for cv_4,...,cv_9, leaving only cv_0,...,cv_3 unknown. Since there are only 2^32 possible values for these four bytes, we can find them by an exhaustive search of 2^48 time without change of the overall time complexity.
This attack can also be converted into a known plaintext attack using 2^49 known plaintexts and essentially the same time complexity.
2. Similar attacks are possible on ciphers which are even more similar to SkipJack, such as SkipJack-(1,16,17) and SkipJack-(16,17,32), but with higher complexities.
Details on these improved results will be given in a forthcoming announcement.